python生成二维码图片

算法视频讲解，非常易懂（若加载失败可点击下方源视频链接）

源视频链接：https://www.youtube.com/watch?v=JLARzu7coEs

举例：

现有如下有向连通图，求出v1到v9的最短距离

算法代码

--定义方法：判断列表是否存在指定元素
	local contains = function(list, element)
		for i = 1, #list do
			if list[i] == element then
				return true
			end
		end
		return false
	end
	
--定义方法：查找目前还未被访问的结点中距离起点最近的结点
local findMinDisNodeNotVisited = function(dis2startNode)
    local minDis = math.maxinteger
    local minDisNode = nil
    for node, visitedAndDis in pairs(dis2startNode) do
        if not visitedAndDis[1] and visitedAndDis[2] >= 0 then
            if visitedAndDis[2] < minDis then
                minDis = visitedAndDis[2]
                minDisNode = node
            end
        end
    end
    return minDisNode
end

--构建图（连通图）
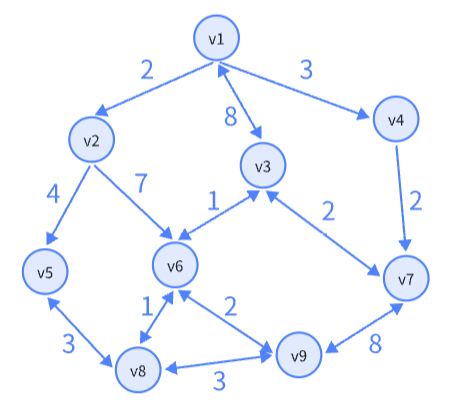
local map = {}
map["v1"] = {["v2"] = 2, ["v3"] = 8, ["v4"] = 3}
map["v2"] = {["v5"] = 4, ["v6"] = 7}
map["v3"] = {["v1"] = 8, ["v6"] = 1, ["v7"] = 2}
map["v4"] = {["v7"] = 2}
map["v5"] = {["v8"] = 3}
map["v6"] = {["v3"] = 1, ["v8"] = 1, ["v9"] = 2}
map["v7"] = {["v3"] = 2, ["v9"] = 8}
map["v8"] = {["v5"] = 3, ["v6"] = 1, ["v9"] = 3}
map["v9"] = {["v6"] = 2, ["v7"] = 8, ["v8"] = 3}

local dis2startNode = {}	--记录每个结点距离起点的最小距离，以及是否被访问过，key为结点名，value[1]为是否被访问过，value[2]为距离，距离 < 0代表无限大
local preNode = {}			--记录每个结点的前面一个结点，key为结点名，value为结点名

local startNode = "v1"		--指定一个起点
local endNode = "v9"		--指定一个终点
local nodeCount = 0			--map的结点数量（由于map是连通图，所以nodeCount等于map的长度）
local curNode = startNode	--存储与起点距离最短的结点
local visitedNodeCount = 0	--记录已访问过的结点数量，用于优化算法时间

--初始化数据
for k, v in pairs(map) do
    nodeCount = nodeCount + 1
    dis2startNode[k] = {false, -1}	--在算法开始前，除起点外，所有结点与起点的距离都初始化为无限大，且包含起点都标记为未访问
end
dis2startNode[startNode][2] = 0	--起点与自己的距离初始化为0

repeat
    curNode = findMinDisNodeNotVisited(dis2startNode)
    --标记curNode为已访问过
    dis2startNode[curNode][1] = true
    visitedNodeCount = visitedNodeCount + 1
    local neighborList = map[curNode]	--获取curNode的邻接点
    for neighborNode, disFromCurNode2neighborNode in pairs(neighborList) do
        if not dis2startNode[neighborNode][1] then
            --判断startNode到curNode的距离 + curNode到neighborNode的距离 是否小于 dis2startNode集合中记录的startNode到neighborNode的距离
            local startNode2curNode = dis2startNode[curNode][2]	--startNode到curNode的距离直接从dis2startNode集合取得
            local startNode2neighborNode = dis2startNode[neighborNode][2]	--获取dis2startNode中记录的从startNode到neighborNode的距离，<0代表无限大
            local isShortPath = startNode2neighborNode < 0 or startNode2curNode + disFromCurNode2neighborNode < startNode2neighborNode

            if isShortPath then
                --更新dis2startNode集合中neighborNode的值
                local newDis = startNode2curNode + disFromCurNode2neighborNode
                dis2startNode[neighborNode][2] = newDis
                --更新preNode集合中的neighborNode的前面点为curNode
                preNode[neighborNode] = curNode
            end
        end
    end
until(visitedNodeCount == nodeCount)	--当图中全部连通结点均被访问过时，算法结束

--在preNode集合中取endNode进行回溯，直到找到startNode，再将这条回溯链路反转即为从startNode到endNode的最短路径
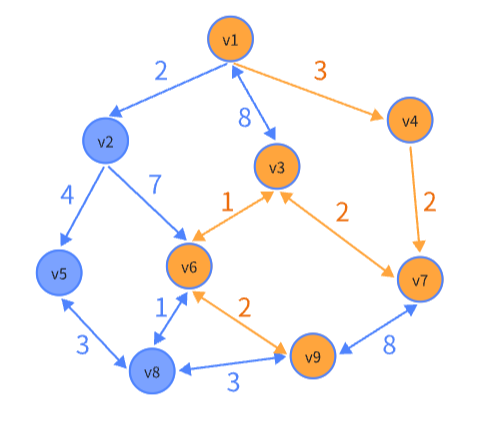
local node = endNode
local path = {node}		--记录最短路径的结点
local length = 0		--总路程
while true do
    local pre_node = preNode[node]
    length = length + map[pre_node][node]
    node = pre_node
    table.insert(path, node)
    if node == startNode then
        break
    end
end

--结果输出
local output = "minimum distance from "..startNode.." to "..endNode .. " is "..length..". path = "
for i = #path, 1, -1 do
    output = output .. path[i] .. " -> "
end
print(string.sub(output, 1, #output - 4))

程序输出：

minimum distance from v1 to v9 is 10. path = v1 -> v4 -> v7 -> v3 -> v6 -> v9

路线演示：